1引言（Introduction）
足式行走的足端轨迹是非连续的，对非结构化地形具有良好的适应能力，在现实环境中具有巨大的应用潜力。其中，四足机器人相对于两足机器人具有良好的稳定性，相对于六足及多足机器人而言结构简单，在军事运输、森林探测、抢险救援等场景具有广阔的应用前景，多年来一直是国内外机器人领域的研究热点之一。目前，国内外代表性的四足机器人研究成果主要有波士顿动力公司（BostonDynamics）的BigDog、LittleDog、LS3、WildCat，麻省理工学院（MIT）的Cheetah，上海交通大学的仿生小象四足机器人，哈尔滨工业大学的类豹型四足机器人，上海大学的XDog，山东大学的液压四足机器人等。从国内外研究成果中可以看出，四足机器人研究的重点在于实现高速、重载、低能耗等运动特性，而腿部结构的设计是其关键影响因素之一。
腿部结构设计主要需要考虑2个要素：驱动方式和腿部结构。本文在调研与分析国内外四足机器人驱动方式与腿部结i构的基础上，结合四足机器人小型化、大负载、低能耗、高效率等需求，针对现有电驱动足式机器人存在的电机驱动需换向、腿部重量比（腿部重量与机器人总重量之比）大、惯量大等问题，提出一种适用于连续电驱动的复合连杆式机器人腿部结构构型，然后对腿部机构进行足端轨迹规划，并以轨迹再现为优化目标对腿部机构结构参数进行优化设计，最后通过虚拟样机仿真与测试平台实验对设计的合理性进行验证。
2四足机器人现有研究分析（Analysisoncurrentquadrupedrobots）
2.1四足机器人驱动方式分析
机器人驱动方式一般分为液压驱动、气压驱动和电驱动，各类驱动方式的特点如表1所示。气压驱动方式的环境适应性、可靠性强，元件结构简单、使用寿命较长，但无法输出精确位移，效率较低、成本高，且由于空气具有可压缩性，系统动态稳定性较差，适用于大质量、小动力的场合。气压驱动存在较大的噪音，且属于需要不断产生气动源的驱动装置，因而其应用范围受到了限制。目前，四足机器人更多采用电驱动和液压驱动。液压驱动方式输出功率较大、惯性小、动作灵敏，可实现负载能力强、控制精度高，但自重与额定负重比一般较大，使得机器人难以小型化。若要实现大功率、小型化，难度与成本极高，且液压系统无法避免产生高噪音。如HyQ机器人的腿部结构由于液压缸的原因导致惯量较大，不适于高速奔跑环境。相比之下，电驱动噪音小、定位准确、调速方便、抗干扰能力强、运行速度平稳，具有较大的过载能力，但电机驱动普遍承载能力较弱。近年来，随着驱动电机的高速发展，驱动力矩的大幅提高，产生了一系列大扭矩电机，使高速电驱动成为小型四足机器人研究的重要方向。

2.2四足机器人腿部结构分析
根据机械结构形式的不同，可以将常见的四足机器人腿部构型分为关节型、连杆型、缩放型等。
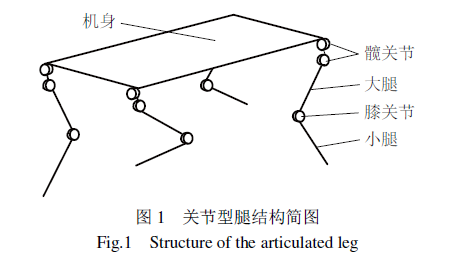
关节型腿部结构直接仿照动物髋关节、膝关节、踝关节等骨骼形式，从外形上看，该类型腿部结构非常接近于动物的四肢，如图1所示。一般由关节式连杆组成，优点在于结构紧凑，运动灵活，腿部足端有较大的运动空间，当运动失稳时具有较强的位姿恢复能力；不足之处在于承载能力较小，通常在关节处安装驱动元件（如电机）来驱动腿部运动，因而腿部关节越多，安装的驱动元件越多，腿部重量越大，惯量也越大，故机器人整体的机动性大大降低。

连杆型腿部结构由多个连杆铰接而成，根据杆之间的连接方式又可分为串联型、并联型和混联型。串联型具有结构简单、运动空间大、控制简单等优点，关节型腿结构也属于串联型连杆腿结构；并联型具有刚度大、承载能力强、精度高及惯性小等优点；混联型则综合了串联型与并联型结构的优点，上海交通大学的仿生小象机器人便采用了混联型连杆腿部构型。本文提及的连杆型主要针对并联型与混联型腿部结构。

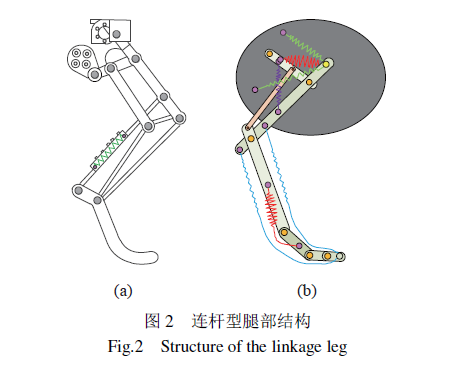
Park受猫后腿骨骼肌肉生理结构启发，设计了一种由9个连杆和1个弹簧组成的单自由度腿部机构，如图2（a）所示。基于该腿部机构研制的机器人能够以0.75m/s的平均速度在平地上奔跑。仿猫式连杆机构腿部结构实现了电机整周连续驱动，但由于单自由度固定的腿部配置难以实现丰富的足端轨迹，因此面对不规则地形时适应性不佳。Cotton将多层智能机械嵌入机器人结构中以降低控制算法的复杂度，基于鸵鸟腿部结构设计了一种高效快速的两足机器人，仿真显示其平地运动速度能够达到34.5km/h，如图2（b）所示。根据鸵鸟腿部尺寸比例缩放，得到了机器人腿部尺寸，并以弹簧代替奔跑时的主要功能肌肉。该机器人每条腿也为单自由度，尚未对机器人腿部足端轨迹进行规划，也未对结构进行优化，且在非结构化地形上的适应性也有待考证。
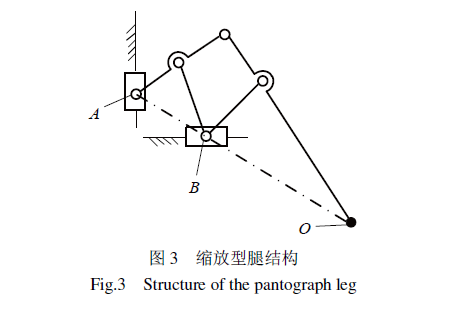
缩放型腿部结构将驱动元件的位移放大至末端执行器，从而使机构的位移增加，与其他结构相比，具有高效性。图3所示为一种典型的四边形缩放机构，利用相似三角形原理，以A点或B点为输入，在O点放大输出。缩放型腿部结构易于通过数学分析规划末端运动轨迹，控制程序编写简单，但该构型构建相似三角形时，常常出现运动输入点、固定铰接点、运动输出点三点共线的情况，导致机架不规则，且安装不便、构型外观不具备仿生特点，作为增益式机构时，缩放型腿部结构体型庞大，不利于机器人小型化，如俄亥俄州立大学研发的ASV（adaptivesuspensionvehicle），长5.2m，宽2.4m，高3.0m，质量为2700kg，负重220kg，负重自重比仅为0.08，整体性能较差。该机构在机器人中具有一定的应用，常见的应用场景如多足步行机器人、工业码垛机器人等。

腿部构型性能特点对比如表2所示，由上述分析可以看出，电驱动具有自重小、调速特性好等特点，有助于提高机器人负重能力、运动效率；连杆型腿部结构相对于关节型腿部结构可将驱动器置于机架减轻腿部重量，相对于缩放型腿部结构安装方便，且杆数多、可优化参数多，有利于实现丰富的足端轨迹。故本文以电驱动作为机器人的驱动方式，采用连杆型腿部构型设计适用于连续电驱动的机器人腿部结构。

3腿部结构设计与足端轨迹规划（Legstructuredesignandfoottrajectoryplanning）
3.1四足机器人腿部机构设计
为实现腿部机构连续电驱动，其驱动关节处应为整转副，故连杆机构中应存在曲柄，且曲柄作为主动件。连杆机构可分为四杆机构和多杆机构。Chebyshev（切比雪夫）机构作为一种经典的四杆机构具有丰富的封闭轨迹，在适当的比例尺寸下能够形成形如人或动物足端的迈步轨迹；五连杆机构是多连杆机构中最基本的一种，其2个自由度相对于单自由度机构具有更大的调节特性，能够实现较复杂的轨迹曲线。考虑到机器人运动过程中步幅的不确定性，要求机器人足端轨迹丰富，本文综合Chebyshev机构与五连杆机构，复合形成机器人腿部足端轨迹生成机构，该复合机构具有2个自由度，相对于四杆机构与五连杆机构拥有更多的设计变量，有利于优化出更多的轨迹特征。

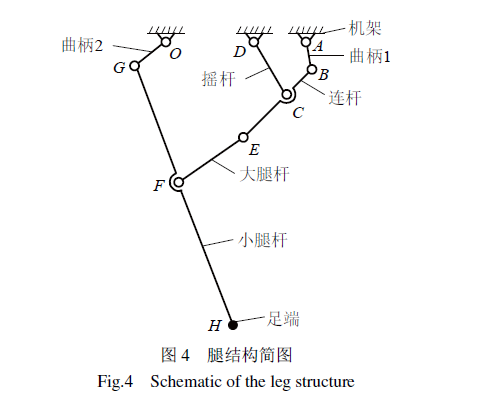
设计的腿部结构简图如图4所示，图中腿部机构连杆分别为：驱动曲柄1（AB）、连杆（BE）、摇杆（CD）、大腿杆（EF）、小腿杆（GH）、辅动曲柄2（OG）。腿部机构为闭链结构，相对于三杆开链结构具有良好的刚度。腿部机构形成2个闭环，第1个闭环为基架、主动曲柄1（AB）、摇杆（CD）、连杆（BE）组成的Chebyshev机构，主动曲柄由电机驱动，连杆（BE）带动大腿杆运动，生成抬腿摇摆运动；第2个闭环为由Chebyshev机构输出连杆（BE）、大腿杆（EF）、小腿杆（GH）、辅动曲柄2（OG）、机架组成的复合五杆机构，辅动曲柄2由电机驱动，复合五杆机构在足端H生成足端轨迹。为便于驱动电机安装以减轻腿部重量，铰接点A、D、O位于机架同一水平线上，点A与点O为驱动电机驱动铰接点。
该腿部机构具有如下优点：
1）丰富的足端轨迹域，众多的结构参数为优化出机器人的腿部机构足端运动轨迹提供了可能。
2）驱动电机安装于机架上，相对于关节式腿部结构，减轻了腿部的质量及转动惯量，低转动惯量腿可以减小摆动相时的力矩需求，在相同驱动力矩下占空系数更大，有利于减小与地面接触的反力，降低能量损耗。
3）该腿部采用复合连杆机构，电机驱动曲柄连续转动，而不必改变电机转动方向实现腿部连续运动，省去了电机换向时间，避免了电机换向产生的冲击及能量损失，特别是高速时，有利于提高能量利用率及运动速率。
3.2足端轨迹规划
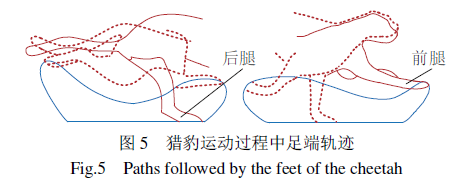
机器人在运动过程中足端在支撑相与摆动相之间重复转换，形成的足端轨迹的步长与步高两个重要特征对机器人的运动效率与越障性能具有重要影响。动物的运动特点为机器人足端轨迹研究提供了参考，美国学者Hildebrand对自然界中运动敏捷的猎豹足端轨迹进行了研究，如图5所示。由图可知，猎豹足端轨迹形成一条封闭的圆滑曲线，在着地时，足端有回缩现象，在离地时，足端有后摆现象，支撑相轨迹为一条直线。机器人足端轨迹规划时，需要考虑运动连续性、效率等诸多问题，例如过大的回缩与后摆将降低运动效率，故不能照搬生物足端轨迹。为了使机器人稳定、高效地行走，足端轨迹规划应满足：（1）足端轨迹应为圆滑封闭的曲线，保证足端运动速度、加速度连续无突变；（2）足端运动与地面无冲击，即着地、离地时速度与加速度为0；（3）尽量避免不必要的运动。

摆动相决定了机器人步长与步高，对机器人的运动性能具有重要影响，支撑相机器人足端与地接触，形成的轨迹多为简单的直线，国内外学者在足端轨迹规划时主要针对摆动相轨迹进行规划。常见的机器人足端轨迹曲线有矩形曲线、椭圆、抛物线、摆线（修正摆线）、心形线、组合线段等，摆线与椭圆函数形式简单、导数连续平滑变化，摆动相的起始角和落地角均为直角，没有水平分量，故不易打滑；行走过程中没有速度突变，能够保证机器人腿在摆动相稳定、无冲击地迈步行走。具有相同对称轴的修正摆线与椭圆的表达式分别如式(1)、(2)所示：

式中L、H、φ分别为步长、步高、极角。

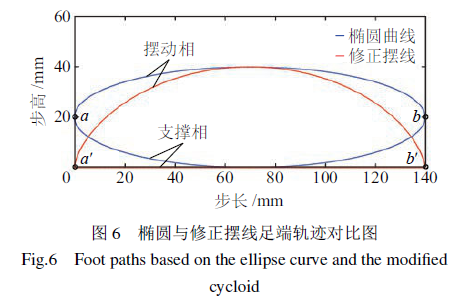
图6是以修正摆线作为摆动相、直线作为支撑相的足端轨迹，和以椭圆曲线为摆动相、支撑相的完整足端轨迹的对比图，图中步长为140mm，步高为40mm。可知，在相同步长与步高下，修正摆线曲线比椭圆短，机器人在一个周期行走中足端经过的轨迹少，减少了不必要的运动，消耗能量少；但在整个轨迹周期中椭圆曲线始终保持圆滑，无突变和尖点，而修正摆线在摆动相与支撑相转换处（图中a′、b′点）出现尖点，使得速度产生突变，从而对腿部机构产生冲击，对机器人运动稳定性产生重大影响。考虑在不打滑的前提下，足端轨迹应尽量减小着地冲击，着地平稳、高效、低能耗，本文主要考虑足端轨迹对机器人运动性能的影响，故采用图6中椭圆曲线作为四足机器人行走过程中的足端轨迹。
4四足机器人腿部机构优化（Legmechanismoptimizationofthequadrupedrobot）
给定四足机器人目标参数（长500mm，宽250mm，高300mm，质量不大于15kg）条件下，在上述腿部结构设计与足端轨迹规划的基础上，以再现所规划的足端轨迹为目标，运用现代优化方法优化出腿部机构尺寸。
4.1腿部机构足端轨迹数学表达
为了便于建立足端轨迹数学模型，将机器人腿部倒立放置，建立xOy全局坐标系、x′Gy′局部坐标系，如图7所示．

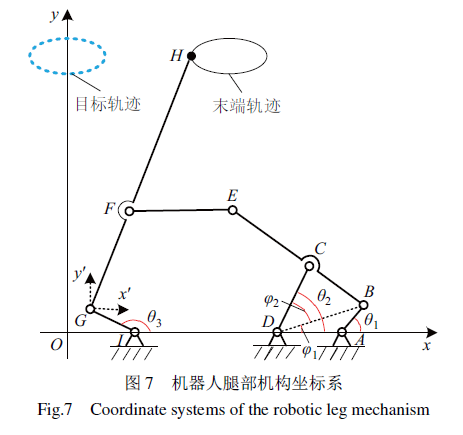
根据机构的运动几何关系可知，当曲柄的位置已知时，足端H点的坐标取决于各个杆件的长度（假设杆AB、BC、CD、AD、BE、EF、GF、GI、ID、FH、OI长度分别为l1；l2；l3；l4；l5；l6；l7；l8；l9；l10；l11）与曲柄角度θ1、θ3。连接BD建立辅助三角形△BCD，为了便于优化过程中运用Matlab软件进行求解（Matlab软件求解反余弦函数时，函数值范围为0至180◦），定义φ1为BD与x轴形成的锐角，φ2为BD与CD的夹角，则：

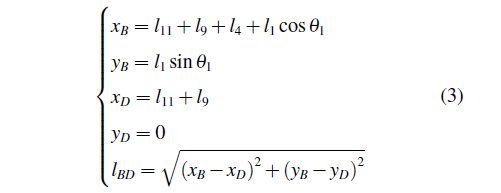
由B点横坐标用、→向量表示l4+l1cosθ1=lBDcosφ1，可得：

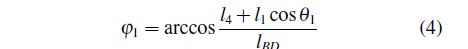
在△BCD中，由余弦定理可得

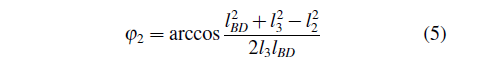
曲柄AB在转动过程中，B点位置可能位于x轴上方（yB>0）或下方（yB<0），在不同的位置处，

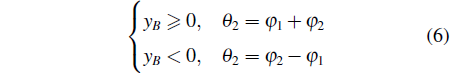
则C点的坐标值为

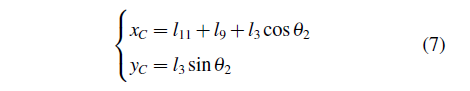
由B、C、E共线与等比分点公式，可得E点在xOy全局坐标系下的坐标

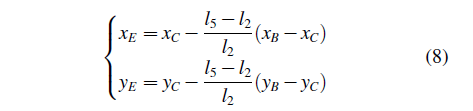
在x′Gy′局部坐标系下，点F是以点G为圆心、以l7为半径的圆与以点E为圆心、以l6为半径的圆的交点之一，即点F的局部坐标是下述方程组的一组解：

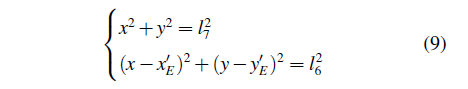
解上式方程组，消去二次项，化简得y的一元二次方程：

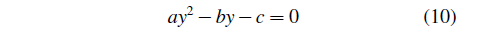
式中：

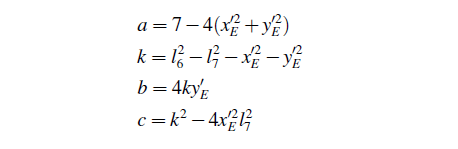
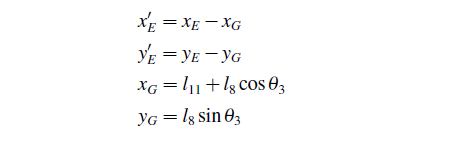
方程(10)的2个根为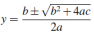，由图示F点在局部坐标系下位置关系y>0及a<0，可知F点的局部坐标为下式解：

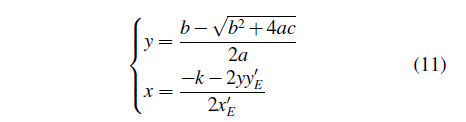
在全局坐标下，F点的坐标为

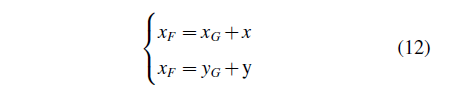
由G、F、H三点共线，及等比分点公式可得

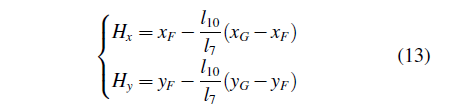
4.2给定轨迹的优化数学模型
1）规划轨迹的数学描述
腿部机构在运动过程中，通过曲柄转动带动足端经过规划的轨迹，因此给定轨迹坐标应与曲柄的转角联系起来．为了便于优化，本文使规划的轨迹相对于y轴对称，如图7中蓝色虚线轨迹，支撑相与摆动相各占半个周期，设定步长L为140mm，步高H为40mm，在全局坐标系下规划的足端轨迹的数学表达式为

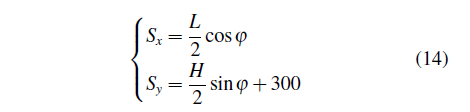
将足端轨迹离散为13个关键点，设定曲柄匀速转动，在规划轨迹上均匀取点，则极角的相位差为30◦，φ=[0◦；30◦；60◦；90◦；120◦；150◦；180◦；210◦；240◦；270◦；300◦；330◦；360◦]。
2）设计变量与目标函数
由4.1节可知，腿部机构足端位置由各组成杆的长度与曲柄位置决定，而曲柄位置由初始位置与转动增量角度确定，曲柄匀速转动时曲柄相对于初始位置转过的角度为Δθ，足端依次经过规划足端轨迹离散的13个点，则Δθ=0◦，30◦，60◦，90◦，120◦，150◦，180◦，210◦，240◦，270◦，300◦，330◦，360◦。由足端轨迹的方向设定曲柄AB顺时针转动、曲柄OG逆时针转动，并以逆时针转动为正，则：

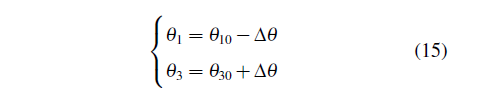
由足端H点坐标推导可知，Hx、Hy坐标都是杆长与曲柄转角的函数，故设计变量取为：x=[l1;l2;l3;l4;l5;l6;l7;l8;l9;l10;l11;θ10;θ20]。曲柄整周转动时足端通过13个点，目标函数使连杆上F点的实际轨迹与给定轨迹之间13个坐标值误差均方根最小，因此目标函数表达式为

式中Sxi、Syi为连杆上H点给定的第i个点坐标，Hxi、Hyi是连杆上H点第i个位置的实际坐标。
3）约束条件
（1）根据腿部总体设计尺寸限制及机构布置情况，各杆长度与曲柄初始位置都有一个上下限范围：

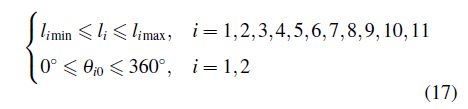
4.3优化分析
本文采用Matlab优化工具箱进行优化，由4.1与4.2节优化数学模型可知，该优化问题属于带约束的非线性优化问题。Matlab的fmincon()函数专门用于求解约束非线性问题，其内点法精度高，收敛性好，但该函数在优化时需要赋初始值。遗传算法适用于任意的优化问题，采用全局寻优，不易陷入局部最优解，且不依靠初值，但遗传算法也存在容易过早收敛、精度不高等缺点。因此，本文优化方法采用遗传算法结合fmincon内点法的方法。优化流程如图8所示，优化计算过程分为2步：第1步，采用遗传算法获得初步优化结果；第2步，以初步优化值作为fmincon函数优化的初始点，进
一步提高优化的精度．运用Matlab编写优化程序，最终优化结果为：x∗=[l∗1，l∗2，l∗3，l∗4，l∗5，l∗6，l∗7，l∗8，l∗9，l∗10，l∗11，θ∗10，θ∗20]T=[20，85.6，130，130，200，159.5，79.6，20，50，209.8，−0.1，55，178.6]T。

5仿真与实验分析（Simulationandexperimentalanalysis）
5.1Adams仿真分析
为简化机器人结构设计与控制，机器人前、后腿都采用了相同的结构，并仿照哺乳动物膝、肘对顶的配置方式。由4.3节优化结果中的各杆长数据，在ProE软件中建立机器人简化3维模型，如图9所示。

将模型导入Adams仿真软件中，设定机器人各构件的材料属性、运动副，并添加驱动，设定驱动的平均转速为72◦/s，固定机身进行机器人单腿运动学仿真，并对足端轨迹进行跟踪，测得足端轨迹并与规划的轨迹进行对比，如图10所示，图中目标曲线为规划的足端轨迹，优化结果曲线为机器人仿真跟踪足端轨迹，由图可知优化结果曲线与目标曲线比较接近。．

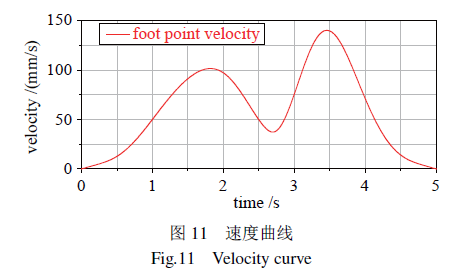
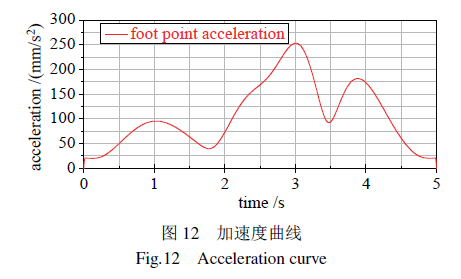
测量机器人单腿在一个步态周期内的速度、加速度曲线，如图11、图12所示，由仿真结果可知，采用规划的椭圆曲线作为足端轨迹可以实现运动过程中轨迹、速度、加速度连续，无突变，且曲线具有较好的平滑性．

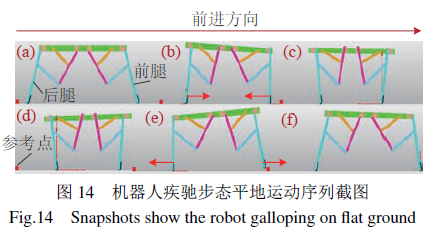
分别采用对角小跑步态、疾驰步态进行机器人运动学仿真，设置驱动转速分别为120◦/s、720◦/s。机器人采用对角小跑步态与疾驰步态的运动序列如图13与图14所示。设定图13中前进方向靠前的腿FL为前左腿、FR为前右腿，靠后的腿HL为后左腿、HR为后右腿。

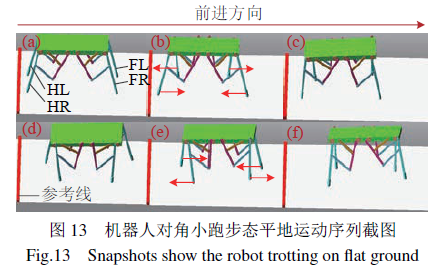
机器人采用对角小跑步态运动时，首先需要进行姿态调整，（a）为机器人初始状态，经过姿态调整后如图（b）所示，前左腿与后右腿组成对角，前右腿与后左腿组成另一对角，2组对角腿依次循环向前、向后迈腿，实现机器人对角小跑步态向前行走运动，如图13（b）～（f）所示。
机器人疾驰步态运动如图14所示，疾驰步态下位于机体前侧的2条腿（或后侧2条腿）的运动姿态相同，设定前进方向靠前的2条腿为前腿，靠后的2条腿为后腿，如图（b）～（f）所示。图（a）为机器人运动前初始状态；图（b）为机器人后腿向前迈步、前腿向后蹬步的状态；随后，后腿处于腾空相、前腿处于支撑相，如图（c）所示；然后，后腿着地、前腿腾空，如图（d）所示；后腿处于支撑相、前腿处于腾空相的状态如图（e）所示。前、后腿依次循环运动，实现机器人向前运动。
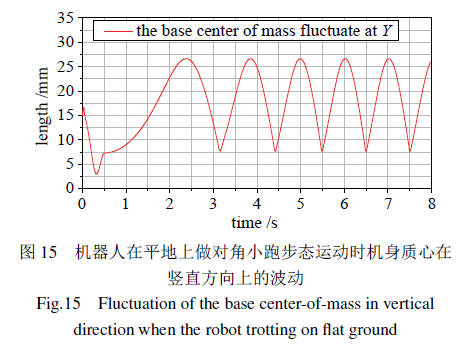
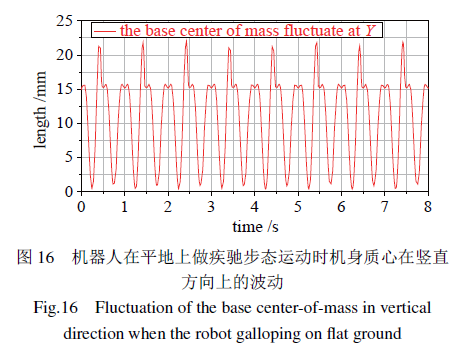
采用对角小跑步态、疾驰步态测得机器人运动过程中机体质心在竖直方向的波动如图15与16所示。图15为对角小跑步态下5个步态周期质心在竖直方向上的波动曲线，从0至1.5s时机器人进行姿态调整，从而形成对角姿态，此过程中质心有一定的波动，1.5s之后机器人以对角小跑步态正常行走，质心在20mm范围内周期性波动。图16为疾驰步态下8个步态周期中质心在竖直方向上的波动曲线，机器人质心在22mm范围内周期性波动。由图分析可知，设计的机器人在2种步态匀速行走状态下质心呈周期性变化，无倾覆发生，具有良好的稳定性，能够实现稳定行走。

5.2实验结果分析
为了验证腿部优化设计结果的可行性，本文采用PLA材料3D打印了机器人腿部构件，并搭建了机器人单腿实验平台，如图17所示。实验平台供电电源采用6V锂电池，驱动电机型号为探索者M05大圆周舵机，控制器为Arduino Mehran H4.60B50.010主控板与Bigfish扩展板。

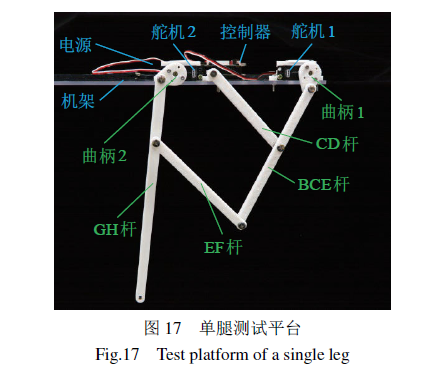
设定曲柄1与曲柄2初始角分别为55◦、178.6◦，通过控制机器人腿部运动，运用尼康D7100相机拍摄了机器人腿部一个周期的运动姿态序列，并用PhotoshopCS6软件将腿部运动照片置于同一图片中，描绘出机器人足端运动轨迹，如图18所示。由图可看出，机器人足端轨迹与仿真轨迹比较接近。已知机器人腿部两曲柄转动中心距离为180mm，绘制图示比例尺，可测出足端轨迹步长约为143mm，步高约为47mm，与Adams仿真中轨迹有微小偏差，造成误差的原因可能是加工与安装误差，使得实际杆长及曲柄初始角度与理论值有一定偏差。

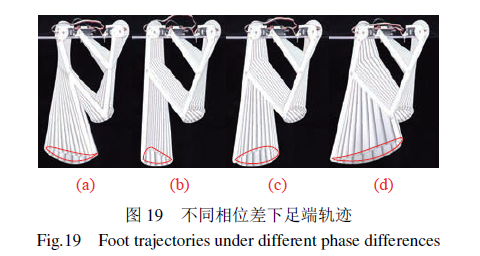
为了验证设计的腿部机构足端轨迹的可调节性，设置驱动曲柄1、曲柄2 在不同初始相位角（即两曲柄的相位差不同）进行测试。图19所示为任意选取曲柄1与曲柄2相位差分别为73◦、124◦、152◦、171◦时的腿部机构末端运动轨迹。由图中可见，两曲柄在不同的相位差下，腿部机构末端具有多样的轨迹曲线，即通过建立电机驱动相位参数与地形参数（如障碍物的高度、宽度）的映射关系可以实现满足不同通过性需求的步幅（步长、步高）输出，这对机器人的地形适应性与实用性具有重要的意义。

6结论（Conclusion）
（1）提出了一种适用于连续电驱动的四足机器人腿部机构方案，采用切比雪夫机构与五连杆机构复合获得了2自由度双曲柄连续整周转动驱动的腿部机构，该机构具有丰富的封闭轨迹，可用于优化机器人在不同步幅下的足端运动轨迹，满足机器人在不同路况下的使用需求。
（2）以规划的机器人足端轨迹再现为优化目标，采用Matlab软件，运用遗传算法与fmincon函数的内点法对机器人腿部机构尺寸进行了优化，获得了满足规划的足端轨迹要求的腿部各杆尺寸和曲柄初始位置。
（3）建立了机器人3维模型，完成了仿真分析。仿真结果表明：规划的足端轨迹能够实现轨迹、速度、加速度连续且无突变；采用对角小跑与疾驰步态进行了机器人运动仿真，实现了2种步态下的行走运动。研制了机器人单腿样机试验平台，进行了足端轨迹跟踪试验，试验结果表明：机器人腿部结构能够实现预定足端轨迹，在不同的电机驱动相位差下足端具有丰富、多样的轨迹，使得腿部结构具有变步幅特性，有利于机器人适应非结构化地形环境。
本文为四足机器人腿部设计提供了新的思路，并为连续电驱动四足机器人研究提供了理论基础。